Question

A random sample of 149 recent donations at a certain blood bank reveals that 76 were type A blood. Does this suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood? Carry out a test of appropriate hypotheses using a significance level of 0.01. Would your conclusion have been different if a significance level of 0.05 has been used?

Answer 1

Yes it suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood.

Well if a significance level of 0.05 is used it will not affect the conclusion

Explanation:

From the question we are told that

The sample size is
`n = 149`

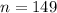
The number that where type A blood is k = 76

The population proportion is
`p = 0.40`

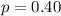
The significance level is
`\alpha = 0.01`

Generally the sample proportion is mathematically represented as

`\r p = (k)/(n)`

=>
`\r p = (76)/(149)`

=>
`\r p = 0.51`

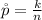
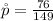
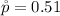
The Null hypothesis is
`H_o : p = 0.41`

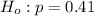
The Alternative hypothesis is
`H_a : p \\e 0.40`

Next we obtain the critical value of
`\alpha` from the z-table.The value is

`Z_(\alpha ) = Z_(0.01) = 1.28`

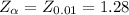
Generally the test statistics is mathematically evaluated as

`t = \frac{\r p - p }{ \sqrt{ (p(1-p))/(n) } }`

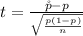
substituting values

`t = \frac{0.51 - 0.40 }{ \sqrt{ (0.40 (1-0.40 ))/(149) } }`

`t =2.74`

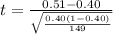
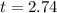
So looking at the values for t and
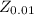`Z_(0.01)` we see that
`t > Z_(0.01)` so we reject the null hypothesis. Which means that there is no sufficient evidence to support the claim

Now if
`\alpha = 0.05` , the from the z-table the critical value for
`\alpha = 0.05` is
`Z_(0.05) = 1.645`

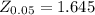
So comparing the value of t and
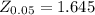`Z_(0.05) = 1.645` we see that
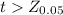`t > Z_(0.05)` hence the conclusion would not be different.