Answer:
we can set the 9 as a benchmark to be the score for the passing grade so that probability of passing a student who guesses every question is less than 0.10
Explanation:
From the given information;
Sample size n = 12
the probability of passing a student who guesses on every question is less than 0.10
In a alternative - response question (true/false) question, the probability of answering a question correctly = 1/2 = 0.5
Let X be the random variable that is represent number of correct answers out of 12.
The X
 BInomial (12, 0.5)
BInomial (12, 0.5)
The probability mass function :
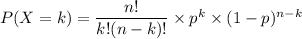
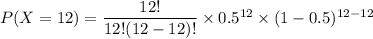
P(X = 12) = 2.44 × 10⁻⁴
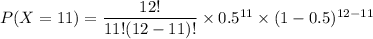
P(X =11 ) = 0.00293
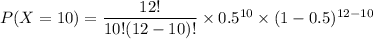
P(X = 10) = 0.01611

P(X = 9) = 0.0537
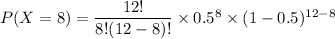
P(X = 8) = 0.12085
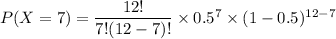
P(X = 7) = 0.19335
.........
We can see that,a t P(X = 9) , the probability is 0.0537 which less than 0.10 but starting from P(X = 8) downwards the probability is more than 0.01
As such, we can set the 9 as a benchmark to be the score for the passing grade so that probability of passing a student who guesses every question is less than 0.10