Question

Based on a​ poll, 40​% of adults believe in reincarnation. Assume that 4 adults are randomly​ selected, and find the indicated probability. Complete parts​ (a) through​ (d) below.Required:a. The probability that exactly 3 of the 4 adults believe in reincarnation is? b. The probability that all of the selected adults believe in reincarnation is? c. The probability that at least 3 of the selected adults believe in reincarnation is? d. If 4 adults are randomly​selected, is 3 a significantly high number who believe in​reincarnation?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

`P(3) = 0.154`

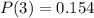
b

`P(4) = 0.026`

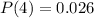
c

`P( X \ge 3 ) = 0.18`

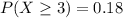
d

option C is correct

Explanation:

From the question we are told that

The probability of success is p = 0.4

The sample size is n= 4

This adults believe follow a binomial distribution is because there are only two outcome one is an adult believes in reincarnation and the second an adult does not believe in reincarnation

The probability of failure is mathematically evaluated as

`q = 1 - p`

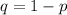
substituting values

`q = 1 - 0.4`

`q = 0.6`

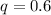
Considering a

The probability that exactly 3 of the selected adults believe in reincarnation is mathematically represented as

`P(3) = \left n} \atop {}} \right. C_ 3 * p^3 * q^(n-3)`

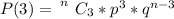
substituting values

`P(3) = \left 4} \atop {}} \right. C_ 3 * (0.40)^3 * (0.60)^(4-3)`

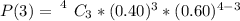
Here
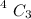`\left 4} \atop {}} \right.C_3` means 4 combination 3 . i have calculated this using a calculator and the value is

`\left 4} \atop {}} \right.C_3 = 4`

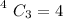
So

`P(3) = 4* (0.4)^3 * (0.6)`

`P(3) = 0.154`

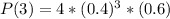
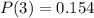
Considering b

The probability that all of the selected adults believe in reincarnation is mathematically represented as

`P(n) = \left n} \atop {}} \right. C_ n * p^n * q^(n-n)`

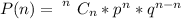
substituting values

`P(4) = \left 4} \atop {}} \right. C_ 4 * (0.40)^4 * (0.60)^(4-4)`

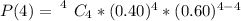
Here
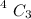`\left 4} \atop {}} \right.C_3` means 4 combination . i have calculated this using a calculator and the value is
`\left 4} \atop {}} \right.C_4 = 1`

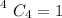
so

`P(4) = 1* (0.4)^4 * 1`

=>
`P(4) = 0.026`

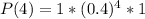
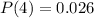
Considering c

the probability that at least 3 of the selected adults believe in reincarnation is mathematically represented as

`P( X \ge 3 ) = P(3 ) + P(n )`

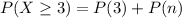
substituting values

`P( X \ge 3 ) = 0.154 + 0.026`

`P( X \ge 3 ) = 0.18`

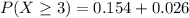
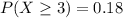
From the calculation the probability that all the 4 randomly selected persons believe in reincarnation is
`p(4) = 0.026 < 0.05`

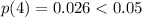
But the the probability of 3 out of the 4 randomly selected person believing in reincarnation is
`P(3) = 0.154 \ which \ is \ > 0.05`

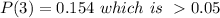
Hence 3 is not a significantly high number of adults who believe in reincarnation because the probability that 3 or more of the selected adults believe in reincarnation is greater than 0.05.