Question

Write an equation for a parabola with a focus of (1,-2) and a directrix of y=6

Answer 1

y = -
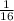`(1)/(16)`(x - 1)² + 2

Explanation:

Any point (x, y) on the parabola is equidistant from the focus and the directrix.

Using the distance formula

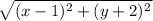`√((x-1)^2+(y+2)^2^)` = | y - 6 |

Square both sides

(x - 1)² + (y + 2)² = (y - 6)² ( expand the factors in y )

(x - 1)² + y² + 4y + 4 = y² - 12y + 36 ( subtract y² - 12y from both sides )

(x - 1)² + 16y + 4 = 36 ( subtract 4 from both sides )

(x - 1)² + 16y = 32 ← subtract (x - 1)² from both sides )

16y = - (x - 1)² + 32 ( divide all terms by 16 )

y = -
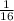`(1)/(16)` (x - 1)² + 2