Answer:
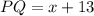
The dimension of the garden is 52.5ft by 43.5ft
Explanation:
Given
The shape above
Required
Determine PQ
Determine dimension of the garden
Calculating Length PQ
Represent the length of the inner rectangle as L
Represent the width of the inner rectangle as W

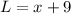
The distance between the inner rectangle and the outer triangle is 4ft
This implies that;
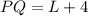
Substitute
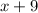 for
for

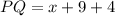
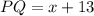
Also;
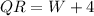
Substitute
 for
for
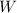
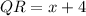
Calculating The Dimension of The Garden
First, we need to determine the Area of the inner rectangle
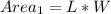
Recall that
 and
and
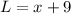
So;
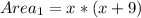
For the bigger rectangle

Recall that
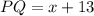 and
and
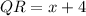
So;

Given that the Area of the walkway is
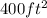
This implies that

Substitute
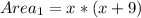 and
and

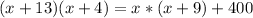
Open All Brackets

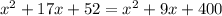
Collect Like Terms

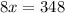
Divide both sides by 8
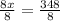

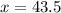
Since the dimensions of the garden is
 and
and
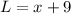
Substitute 43.5 for x in both cases
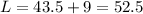
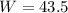
Hence, the dimension of the garden is 52.5ft by 43.5ft