Answer:
a)

b)
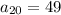
c) term number 17 is the one that gives a value of 40
Explanation:
a)
The sequence seems to be arithmetic, and with common difference d = 3.
Notice that when you add 3 units to the first term (-80, you get :
-8 + 3 = -5
and then -5 + 3 = -2 which is the third term.
Then, we can use the general form for the nth term of an arithmetic sequence to find its simplified form:
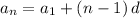
That in our case would give:

b)
Therefore, the term number 20 can be calculated from it:
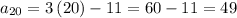
c) in order to find which term renders 20, we use the general form we found in step a):
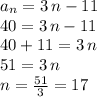
so term number 17 is the one that renders a value of 40