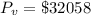Answer:
The value of annuity is
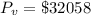
Explanation:
From the question we are told that
The periodic payment is
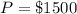
The interest rate is
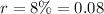
Frequency at which it occurs in a year is n = 2 (semi-annually )
The number of years is
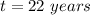
The value of the annuity is mathematically represented as
![P_v = P * [1 - (1 + (r)/(n) )^(-t * n) ] * [((1 + (r)/(n) ))/( (r)/(n) ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/l8zgnvyylyqosz29wui9pyg89hjvp9xk3u.png) (reference EDUCBA website)
(reference EDUCBA website)
substituting values
![P_v = 1500 * [1 - (1 + (0.08)/(2) )^(-22 * 2) ] * [((1 + (0.08)/(2) ))/( (0.08)/(2) ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/8rk2ftsz76eemx4leuiwhtqq15yta0bqx7.png)
![P_v = 1500 * [1 - (1.04 )^(-44) ] * [((1.04 ))/(0.04) ]](https://img.qammunity.org/2021/formulas/mathematics/college/y8ycwta47tkoe8unpjexpzwaxh64r60z6a.png)
![P_v = 1500 * [1 - 0.178 ] * [((1.04 ))/(0.04) ]](https://img.qammunity.org/2021/formulas/mathematics/college/e8aoye5nnmjrtwck92nxmx4y5vydivd5i9.png)