Question

Find the area of the shaded region

Answer 1

`\mathsf{ {5x}^(2) + 28x + 21}`

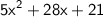
Option A is the right option.

Explanation:

Let's find the area of large rectangle:

`\mathsf{(3x + 6)(2x + 4)}`

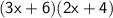
Multiply each term in the first parentheses by each term in the second parentheses

`\mathsf{ = 3x(2x + 4) + 6(2x + 4)}`

Calculate the product

`\mathsf{ = 6 {x}^(2) + 12x + 12x + 6 * 4}`

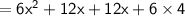
Multiply the numbers

`\mathsf{ = 6 {x}^(2) + 12x + 12x + 24}`

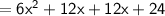
Collect like terms

`\mathsf{ = {6x}^(2) + 24x + 24}`

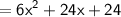
Let's find the area of small rectangle

`\mathsf{(x - 3)(x - 1)}`

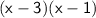
Multiply each term in the first parentheses by each term in the second parentheses

`\mathsf{ = x( x - 1) - 3(x - 1)}`

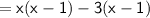
Calculate the product

`\mathsf{ = {x}^(2) - x - 3x - 3 * ( - 1)}`

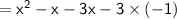
Multiply the numbers

`\mathsf{ = {x}^(2) - x - 3x + 3}`

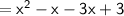
Collect like terms

`\mathsf{ = {x}^(2) - 4x + 3}`

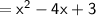
Now, let's find the area of shaded region:

Area of large rectangle - Area of smaller rectangle

`\mathsf{6 {x}^(2) + 24x + 24 - ( {x}^(2) - 4x + 3)}`

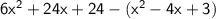
When there is a ( - ) in front of an expression in parentheses, change the sign of each term in the expression

`\mathsf{ = {6x}^(2) + 24x + 24 - {x}^(2) + 4x - 3}`

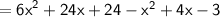
Collect like terms

`\mathsf{ = {5x}^(2) + 28x + 21}`

Hope I helped!

Best regards!