Question

the length of diagonal of a rectangular field is 23.7 m and one of its sides is 18.8 m. find the perimeter of the field.​

Answer 1

Approximately 66.4 Meters

Explanation:

So we have a rectangle with a width of 18.8 meters and a diagonal with 23.7 meters. To find the perimeter, we need to find the length first. Since a rectangle has four right angles, we can use the Pythagorean Theorem, where the diagonal is the hypotenuse.

`a^2+b^2=c^2`

Plug in 18.8 for either a or b. Plug in the diagonal 23.7 for c.

`(18.8)^2+b^2=23.7^2\\b^2=23.7^2-18.8^2\\b=√(23.7^2-18.8^2) \\b\approx14.4 \text{ meters}`

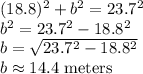
Therefore, the length is 14.4 meters. Now, find the perimeter:

`P=2l+2w\\P=2(14.4)+2(18.8)\\P=66.4\text{ meters}`