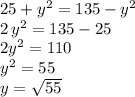Answer:
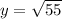
which agrees with answer A
Explanation:
Notice there are three right angle triangles for which we can apply the Pythagorean theorem:
In the small triangle at the bottom we have the Pythagorean theorem rendering:
(a)
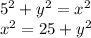
in the second right angle triangle on top of the previous one, if we call the vertical side on the right side "z", we have:
(b)
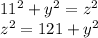
and finally in the large right angle triangle:
(c)
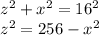
We can combine equations b and c to obtain:
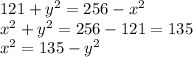
and then combine this and (a) to get: