Question

The length of a rectangle is 7 meters longer than its width. What is the width of this rectangle if its perimeter is equal to 86 meters?

Answer 1

18 meters

Explanation:

Given,

Let length of a rectangle be ' x + 7 ' meters

Let width of a rectangle be ' x ' meters

Perimeter = 86 meters

Now, let's find the width of the rectangle:

Perimeter of rectangle =
`2(l + b)`

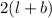
plug the values

`86 = 2(x + 7 + x)`

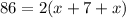
Collect like terms

`86 = 2(2x + 7)`

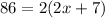
Distribute 2 through the parentheses

`86 = 4x + 14`

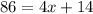
Move constant to R.H.S and change its sign

`86 - 14 = 4x`

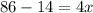
Calculate the difference

`72 = 4x`

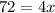
Swipe the sides of the equation

`4x = 72`

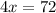
Divide both sides of the equation by 4

`(4x)/(4) = (72)/(4)`

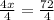
Calculate

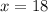`x = 18` meters

Hope this helps..

Best regards!!

Answer 2

18 meters

Explanation:

If the width is w, the length is w + 7.

Perimeter = 2(width + length), therefore:

86 = 2(w + w + 7)

86 = 2(2w + 7)

43 = 2w + 7

36 = 2w

w = 18