Question

an attempt to estimate the height of a tree the Shadow of an upright metre rule was found to be 25 cm and the length of the Shadow of the tree was 7 m what is the height of the tree​

Answer 1

The actual height of the tree is 28 m

Step-by-step explanation:

The given information are;

The length of the shadow of an upright meter rule = 25 cm

The actual height of the meter rule = 100 cm

The length of the shadow of the tree = 7 m

The actual height of the tree = h

We have

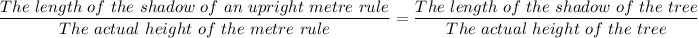`(The \ length \ of \ the \ shadow \ of \ an \ upright \ metre \ rule)/(The \ actual \ height \ of \ the \ metre \ rule) = (The \ length \ of \ the \ shadow \ of \ the \ tree)/(The \ actual \ height \ of \ the \ tree)`Which gives;

`(25 \ cm)/(100 \ cm) = (7 \ m)/(The \ actual \ height \ of \ the \ tree)`

Therefore;

`The \ actual \ height \ of \ the \ tree = 7 \ m * (100 \ cm)/(25\ cm) = 7 \ m * 4 = 28 \ m`

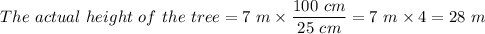
That is the actual height of the tree = 28 m.