Question

One positive integer is 6 less than twice another. The sum of their squares is 801. Find the integers

Answer 1

`\large \boxed{\sf 15 \ \ and \ \ 24 \ \ }`

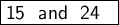
Explanation:

Hello,

We can write the following, x being the second number.

`(2x-6)^2+x^2=801\\\\6^2-2\cdot 6 \cdot 2x + (2x)^2+x^2=801\\\\36-24x+4x^2+x^2=801\\\\5x^2-24x+36-801=0\\\\5x^2-24x-765=0\\\\`

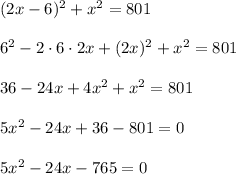
Let's use the discriminant.

`\Delta=b^4-4ac=24^2+4*5*765=15876=126^2`

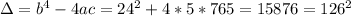
There are two solutions and the positive one is

`(-b+√(b^2-4ac))/(2a)=(24+126)/(10)=(150)/(10)=15`

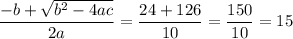
So the solutions are 15 and 15*2-6 = 30-6 = 24

Hope this helps.

Do not hesitate if you need further explanation.

Thank you