Question

How is this question solved?

Answer 1

35.805 that’s the answer good luck

Answer 2

`\large \boxed{\sf \ \ 35.805 \ \ }`

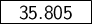
Explanation:

Hello,

First of all we need to find the intersection points of y = 12 and

`y=f(x)=e^x+e^(-x)`

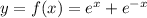
We need to solve the following equation.

`e^x+e^(-x)=12\\\\\text{*** We multiply by }e^x\text{ both side ***}\\\\\left(e^x\right)^2+1=12e^x\\\\\text{*** Let's note } X =e^x\text{, it comes *** }\\\\X^2-12X+1=0`

`\Delta=b^2-4ac=12^2-4=140=2^2\cdot 35\\\\X_1=(12-2√(35))/(2)=6-√(35)\\\\X_2=(12+2√(35))/(2)=6+√(35)\\`

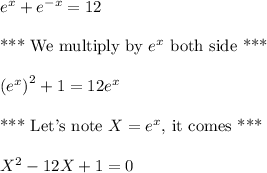
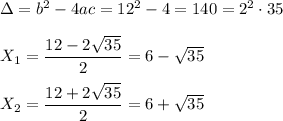
And, we take the greater solution to solve:

`X=e^x=6+√(35)<=>\boxed{x=ln(6+√(5))}`

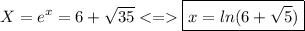
Let's note it a.

Let's compute the integral.

We need to compute the following (because 12-f(x) is pair the integral that we are looking for is)

`\displaystyle 2\int\limits^a_(0) {\left(12-(e^x+e^(-x))\right)} \, dx =12*(2a)-2\int\limits^a_(0) {(e^x+e^(-x))} \, dx \\\\=24a-2[e^x-e^(-x)]_(0)^a=24a-2(e^a-e^(-a))`

We can replace a by the value we already found.

`24\cdot ln(6+√(35))-2\left( 6+√(35)-(1)/(6+√(35))\right)\\\\=24\cdot ln(6+√(35))-2\left(6+√(35)-(√(35)-6)/((√(35)-6)(√(35)+6))\right)\\\\=24\cdot ln(6+√(35))-2\left((29*6+29*√(35)-√(35)+6)/(29)\right)\\\\\\=24\cdot ln(6+√(35))-2\left((180+28√(35))/(29)\right)\\\\`

= 59.46933...-26.66432...=35.8050...

So the answer is
`\boxed{\sf \ \ 35.805 \ \ }`

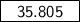
Hope this helps.

Do not hesitate if you need further explanation.

Thank you