Question

11) $ 8,000 is invested in an account that yields 6% interest per year. After how many years will the account be worth 13709.60$ if the interest is compounded monthly?

Answer 1

`\large \boxed{\sf \ \ 9\text{ years} \ \ }`

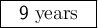
Explanation:

Hello,

First of all, a few remarks:

>>> 1 year is 12 months, right?

>>> Monthly compounding means that each month we compute the interest and they will be included in the investment for the next month.

>>> 6% is an interest per year, it means that to compute the interest for 1 month we need to compute by 6% multiplied by
`(1)/(12)`

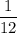
Let's do it !

At the beginning, we have:

$8,000

After 1 month, we will have:

`8000 + 8000\cdot (6\%)/(12)=8000\cdot (1+ (6)/(1200))= 8000\cdot (1+ (1)/(200))`

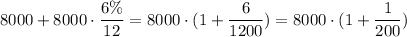
After 2 months, we will have:

`8000\cdot (1+ (1)/(200))\cdot (1+ (1)/(200))=8000\cdot \left(1+ (1)/(200)\right)^2`

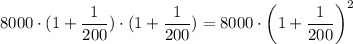
After n months, we will have

`8000\cdot \left(1+ (1)/(200)\right)^n=8000\cdot \left(1.005\right)^n`

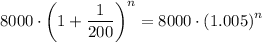
We are looking for n such that

`8000\cdot \left(1.005\right)^n=13709.60\\\\ln(8000)+ n\cdot ln(1.005)=ln(13709.60)\\\\\\n = (ln(13709.60)-ln(8000))/(ln(1.005))=108`

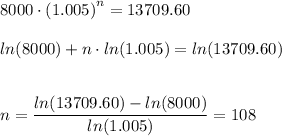
So, we need 108 months to reach this amount, which means 108/12=9 years.

Hope this helps.

Do not hesitate if you need further explanation.

Thank you