Question

Please answer this question now

Answer 1

`Area = 400.4 m^2`

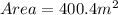
Explanation:

Given:

∆UVW,

m < U = 33°

m < V = 113°

VW = u = 29 m

Required:

Area of ∆UVW

Solution:

Find side length UV using Law of Sines

`(u)/(sin(U)) = (w)/(sin(W))`

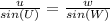
U = 33°

u = VW = 29 m

W = 180 - (33+113) = 34°

w = UV = ?

`(29)/(sin(33)) = (w)/(sin(34))`

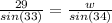
Cross multiply

`29*sin(34) = w*sin(33)`

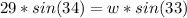
Divide both sides by sin(33) to make w the subject of formula

`(29*sin(34))/(sin(33)) = (w*sin(33))/(sin(33))`

`(29*sin(34))/(sin(33)) = w`

`29.77 = w`

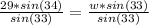
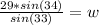
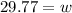
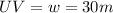`UV = w = 30 m` (rounded to nearest whole number)

Find the area of ∆UVW using the formula,

`area = (1)/(2)*u*w*sin(V)`

`= (1)/(2)*29*30*sin(113)`

`= (29*30*sin(113))/(2)`

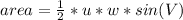
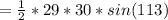
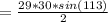
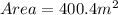`Area = 400.4 m^2` (to nearest tenth).