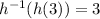Answer:
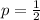
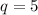
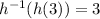
Explanation:
Given
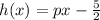
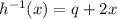
Solving for p and q
Replace h(x) with y in
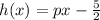
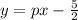
Swap the position of y and d

Make y the subject of formula
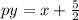
Divide through by p
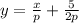
Now, we've solved for the inverse of h(x);
Replace y with

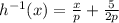
Compare this with
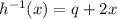
We have that
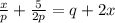
By direct comparison
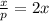 --- Equation 1
--- Equation 1
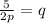 --- Equation 2
--- Equation 2
Solving equation 1
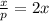
Divide both sides by x
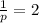
Take inverse of both sides
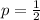
Substitute
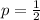 in equation 2
in equation 2
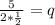

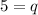
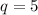
Hence, the values of p and q are:
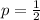 ;
;
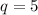
Solving for
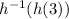
First, we'll solve for h(3) using
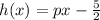
Substitute
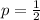 ; and
; and
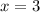
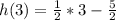
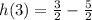
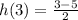
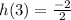
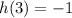
So;
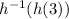 becomes
becomes
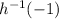
Solving for
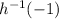 using
using
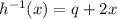
Substitute
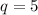 and
and
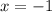
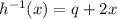 becomes
becomes
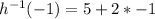

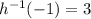
Hence;