Question

The JUST-SAY-MOW lawn mowing company consists of two people: Marsha and Bob. If Marsha cuts the lawn by herself, she can do it in 3 hours. If Bob cuts the same lawn himself, it takes him an hour longer than Marsha. How long would it take them if they worked together? Round to the nearest hundredth of an hour.

Answer 1

it will take them 1.71 hours to finish cutting the lawn if they work together.

Explanation:

If Marsha cuts the lawn by herself it will take her 3 hours, this mean that in one hour she cuts 1/3 of the lawn.

On the other hand Bob needs one more hour to finish the lawn, this means it takes him 4 hours to cut it and therefore he cuts 1/4 of the lawn per hour.

Now, to know how much they cut by working together we need to sum up the amount of lawn they cut per hour:

Working together in one hour: Marsha's one hour + Bob's one hour

Working together in one hour:
`(1)/(3)+ (1)/(4)=(4+3)/(12)=(7)/(12)`

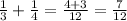
Therefore, working together they will cut 7/12 in one hour.

Now, to know how long will it take it to cut the entire lawn (which is equivalent to 12/12), we can write this in terms of proportions

Time Total amount of lawn

1 hour 7/12

x hours 12/12

Solving for x (to know the amount of hours it will take them) we have:

`x=(12)/(12)`÷
`(7)/(12)`=
`1`×
`(12)/(7)=(12)/(7)=1.714`

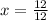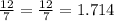
Rounded to the nearest hundredth, we have that working together it will take them 1.71 hours to finish cutting the lawn.