Answer:
6.0 ×
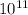 W/
W/
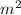
Step-by-step explanation:
From Wien's displacement formula;
Q = e A
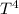
Where: Q is the quantity of heat transferred, e is the emissivity of the surface, A is the area, and T is the temperature.
The emissive intensity =
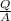 = e
= e
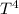
Given from the question that: e = 0.6 and T = 1000K, thus;
emissive intensity = 0.6 ×
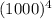
= 0.6 × 1.0 ×
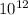
= 6.0 ×
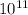
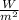
Therefore, the emissive intensity coming out of the surface is 6.0 ×
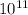 W/
W/
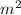 .
.