Question

Urgent, It is a Calculus question and I’ll appreciate your help. Thanks

Answer 1

`\large \boxed{\sf \ \ \pi r^2 \ \ }`

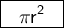
Explanation:

Hello,

We will follow the instructions and then we need first to find the area of any regular n-gon.

I attached one graph so that it is easier to understand.

The n-gon can be divided in n similar isosceles triangles.

So we can find the area of one of these triangles and then multiply by n to get the total area, right?

Let's focus on the triangle OAB then. OA = OB = r, right?

The area of this triangle is the (altitude * AB ) / 2

The angle AOB is
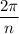`(2\pi)/(n)` by construction of the regular n-gon.

So half this angle is
`(\pi)/(n)` and we can use cosine rule to come up with the altitude:

`\boxed{ altitude = r\cdot cos((\pi)/(n)) }`

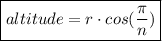
Using the sine rule we can write that

`\boxed{ AB=2r\cdot sin{(\pi)/(n)} }`

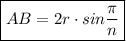
So, the area of the triangle is

`(1)/(2)\cdot r\cdot cos((\pi)/(n)) } \cdot 2r\cdot sin((\pi)/(n))\\\\=r^2\cdot cos((\pi)/(n))\cdot sin((\pi)/(n))`

Ok, but wait, we know how to simplify. We can use that

`sin(2\theta)=2cos(\theta)sin(\theta)`

So it gives that the area of one triangle is:

`(1)/(2)r^2sin((2\pi)/(n))`

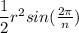
Last step, we need to multiply by n.

`\large \boxed{\sf \ \ A(n)=(1)/(2)nr^2sin((2\pi)/(n)) \ \ }`

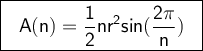
Now, let's use a result from Calculus:

`\displaystyle \lim_(x\rightarrow0) (sin(x))/(x)=1`

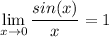
How to use it here? Just notice that

`\displaystyle \lim_(n\rightarrow +\infty) (sin((2\pi)/(n)))/((2\pi)/(n))=1\\\\\lim_(n\rightarrow +\infty) (n)/(2\pi)sin((2\pi)/(n))=1\\\\\lim_(n\rightarrow +\infty) nsin((2\pi)/(n))=2\pi`

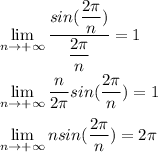
So, finally

`\Large \boxed{\sf \lim_(n\rightarrow +\infty) A(n)=(1)/(2)r^22\pi=\pi r^2 }`

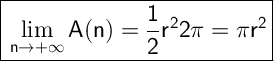
Hope this helps.

Do not hesitate if you need further explanation.

Thank you