Answer:
The probability that the sample proportion will be greater than 13% is 0.99693.
Explanation:
We are given that a large shipment of laser printers contained 18% defectives. A sample of size 340 is selected.
Let
 = the sample proportion of defectives.
= the sample proportion of defectives.
The z-score probability distribution for the sample proportion is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where, p = population proportion of defective laser printers = 18%
n = sample size = 340
Now, the probability that the sample proportion will be greater than 13% is given by = P(
 > 0.13)
> 0.13)
P(
 > 0.13) = P(
> 0.13) = P(
 >
>
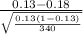 ) = P(Z > -2.74) = P(Z < 2.74)
) = P(Z > -2.74) = P(Z < 2.74)
= 0.99693
The above probability is calculated by looking at the value of x = 2.74 in the table which has an area of 0.99693.