Question

Suppose a stock has an expected return of 12% and a standard deviation of 6%. What is the likelihood that this stock returns between 12% and 18%

Answer 1

Answer: 34.13%.

Step-by-step explanation:

Given : Expected return :
`\mu=12\%=0.12`

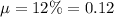
Standard deviation:
`\sigma=6\%=0.06`

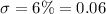
Let x be the stock returns.

Then, the probability that stock returns between 12% and 18%:

`P(0.12<x<0.18)=P((0.12-0.12)/(0.06)<(x-\mu)/(\sigma)<(0.18-0.12)/(0.06))\\\\=P(0<Z<1)\ \ \ [\because z=(x-\mu)/(\sigma)]\\\\=P(Z<1)-P(Z<0)\\\\=0.8413-0.5\ \ \ \text{[By z-table]}\\\\=0.3413`

Hence, the likelihood that this stock returns between 12% and 18% is 34.13%.