Question

The tens digit in a two digit number is 4 greater than one’s digit. If we interchange the digits in the number, we obtain a new number that, when added to the original number, results in the sum of 88. Find this number

Answer 1

The original digit is 62

Explanation:

Let the Tens be represented with T

Let the Units be represented with U

Given:

Unknown Two digit number

Required:

Determine the number

Since, it's a two digit number, then the number can be represented as;

`T * 10 + U`

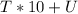
From the first sentence, we have that;

`T = 4 + U`

`T = 4+U`

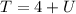
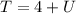
Interchanging the digit, we have the new digit to be
`U * 10 + T`

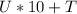
So;

`(U * 10 + T) + (T * 10+ U) = 88`

`10U + T + 10T + U= 88`

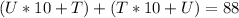
Collect Like Terms

`10U + U + T + 10T = 88`

`11U + 11T = 88`

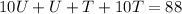
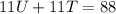
Divide through by 11

`U + T = 8`

Recall that
`T = 4+U`

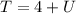
`U + T = 8` becomes

`U + 4 + U = 8`

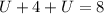
Collect like terms

`U + U = 8 - 4`

`2U = 4`

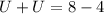
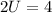
Divide both sides by 2

`U = 2`

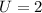
Substitute 2 for U in
`T = 4+U`

`T = 4 + 2`

`T = 6`

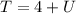
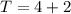
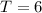
Recall that the original digit is
`T * 10 + U`

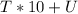
Substitute 6 for T and 2 for U

`T * 10 + U`

`6 * 10 + 2`

`60 + 2`

`62`

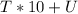
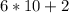
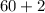
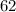
Hence, the original digit is 62