Question

Simon has 160160160 meters of fencing to build a rectangular garden. The garden's area (in square meters) as a function of the garden's width xxx (in meters) is modeled by A(x)=-x(x-80)A(x)=−x(x−80)A, left parenthesis, x, right parenthesis, equals, minus, x, left parenthesis, x, minus, 80, right parenthesis What width will produce the maximum garden area?

Answer 1

The maximum area is 1600 sq meters.

Explanation:

The garden's area is modeled by a quadratic function, whose graph is a parabola.

The maximum area is reached at the vertex.

So in order to find the maximum area, we need to find the vertex's y-coordinate.

We will start by finding the vertex's x-coordinate, and then plug that into A(x).

The vertex's x-coordinate is the average of the two zeros, so let's find those first.

A(x)=0 -x(x-80)=0

↓ ↓

-x=0 or x-80=0

x=0 or x=80

Now let's take the zeros' average:

`((0)+(80))/(2)=(80)/(2)=40`

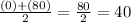
The vertex's x-coordinate is 40. Now lets find A(40):

A(40)= -(40)(40-80)

= -(40)(-40)

= 1600

in conclusion, the maximum area is 1600 square meters.