Answer:
See Explanation below
Explanation:
This question has missing details because the number of video games is not stated;
However, you'll arrive at your answer if you follow the steps I'll highlight;
The question requests for the number of arrangement; That means we're dealing with permutation
Let's assume the number of video games is n;
To arrange n games, we make use of the following permutation formula;
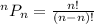
Simplify the denominator
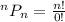
0! = 1; So, we have
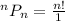

Now, let's assume there are 3 video games;
This means that n = 3
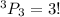
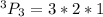
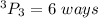
So, whatever the number of video games is; all you have to do is; substitute this value for n;