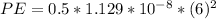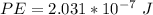Question

A cylindrical capacitor is made of two thin-walled concentric cylinders. The inner cylinder has radius 5 mm , and the outer one a radius 11 mm . The common length of the cylinders is 160 m . What is the potential energy stored in this capacitor when a potential difference 6 V is

Answer 1

The potential energy is
`PE = 2.031 *10^(-7) \ J`

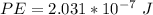
Step-by-step explanation:

From the question we are told that

The inner radius is
`r_i = 5 \ mm = 0.005 \ m`

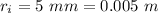
The outer radius is
`r_o = 11 \ mm = 0.011 \ m`

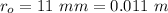
The common length is
`l = 160 \ m`

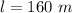
The potential difference is
`V = 6 \ V`

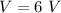
Generally the capacitance of the cylindrical capacitor is mathematically represented as

`C = (2 \pi * k * \epsilon_o )/( ln ( r_o )/(r_i) ) * l`

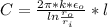
Where
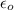`\epsilon _o` is the permitivity of free space with the values
`\epsilon _o = 8.85*10^(-12) \ m^(-3) \cdot kg^(-1)\cdot s^4 \cdot A^2`

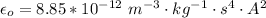
and k is the dielectric constant of the dielectric material here the dielectric material is free space so k = 1

Substituting values

`C = (2* 3.142 * 1 * 8.85*10^(-12) )/( ln ( 0.011)/(0.005) ) * 160`

`C = 1.129 *10^(-8) \ F`

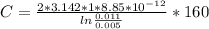
The potential energy stored is mathematically represented as

`PE = (1)/(2) * C * V ^2`

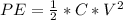
substituting values

`PE = 0.5 * 1.129 *10^(-8) * (6)^2`

`PE = 2.031 *10^(-7) \ J`