Answer:
If
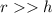 , the slang height of the cone is approximately 23.521 inches.
, the slang height of the cone is approximately 23.521 inches.
Explanation:
The surface area of a cone (A) is given by this formula:
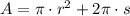
Where:
 - Base radius of the cone, measured in inches.
- Base radius of the cone, measured in inches.
 - Slant height, measured in inches.
- Slant height, measured in inches.
In addition, the slant height is calculated by means of the Pythagorean Theorem:
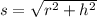
Where
 is the altitude of the cone, measured in inches. If
is the altitude of the cone, measured in inches. If
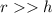 , then:
, then:
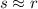
And:

Given that
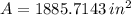 , the following second-order polynomial is obtained:
, the following second-order polynomial is obtained:
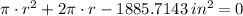
Roots can be found by the Quadratic Formula:
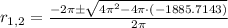
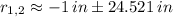
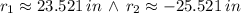
As radius is a positive unit, the first root is the only solution that is physically reasonable. Hence, the slang height of the cone is approximately 23.521 inches.