Question

The instruction booklet for your pressure cooker indicates that its highest setting is 11.5 psi . You know that standard atmospheric pressure is 14.7 psi, so the booklet must mean 11.5 psi above atmospheric pressure. At what temperature in degrees Celsius will your food cook in this pressure cooker set on "high"

Answer 1

16.83°

Step-by-step explanation:

The computation of temperature in degrees is shown below:

For this we need to applied the combination of the Clasius Clapyeron equation which is

`ln((P_2)/(P_1)) = (-\Delta Hvap)/(R) * ((1)/(T_2)- (1)/(T_1))`

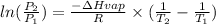
Where

P_2 and P_1 represents the pressure of vapor at point 1 and 2

dH = Here we use J/mol

R = 8.314 J/mol K

T1 and T2 represent the temperature of Saturation temperature for point 1 and 2

Now

we have to change the negative signs

i.e

`ln((P_2)/(P_1)) = (\Delta Hvap)/(R) * ((1)/(T_1)- (1)/(T_2))`

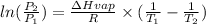
As we know that

dHvap for water = 40.67 kJ/mol

T1 = 373 K,

T2 = x

P1 = 14.7 psi;

P2 = 11.2 + 14.7 = 25.9 psi

Now put the values to the above formula

So,

`ln ((25.9)/(14.7)) = (40670)/(8.314) * ((1)/(373)- (1)/(T_2))\\\\T_2 = - (ln ((25.9)/(14.7))* (8.314)/(40670) - (1)/(373))^(-1)`

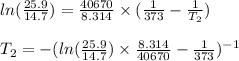
After solving this

T_2 = 389.836K

T_2 = 389.836 - 273

T_2 = 116.836 °C

Therefore by 16.83°, it becomes higher