Answer:
Area = 19.9 mm²
Explanation:
Step 1: Find Angle V.
m < V = 180 - (131 + 27) (sum of angles in a triangle)
V = 22°
Step 2: Find UW using the law of sines.
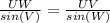
Plug in your values
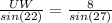
Multiply both sides by sin(22) to solve for UW
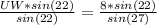
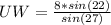
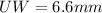
Step 3: Find the area of ∆UVW
Area = ½*UW*UV*Sin(U)
Area = ½*6.6*8*sin(131)
Area = 3.3*8*sin(131)
Area = 19.9 mm² (to the nearest tenth)