Question

What is the line of symmetry for the parabola whose equation is y=-x^2-x+2

Answer 1

`\huge \boxed{\sf \ \ x=-(1)/(2) \ \ }`

Explanation:

Hello,

We need to express this parabola using this kind of expression

`y=a(x-b)^2+c`

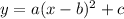
and then, the line of symmetry will be the line x = b

Let's do it !

`\text{*** Complete the square ***} \\ \\ x^2+x=x+2\cdot (1)/(2)\cdot x=(x+(1)/(2))^2-(1^2)/(2^2)=(x+(1)/(2))^2-(1^2)/(4) \\ \\ \text{*** Apply it to our parabola } \\ \\y=-x^2-x+2=-(x^2+x)+2=-[(x+(1)/(2))^2-(1)/(4)]+2 = -(x+(1)/(2))^2+(1+2*4)/(4)= -(x+(1)/(2))^2+(9)/(4) \\ \\ \text{*** It comes ***} \\ \\ \Large \boxed{\sf \ \ y=-(x+(1)/(2))^2+(9)/(4) \ \ }`

So the line of symmetry is

`\huge \boxed{\sf \ \ x=-(1)/(2) \ \ }`

Hope this helps.

Do not hesitate if you need further explanation.

Thank you