Question

Marie is saving money for home repairs. So far, she has saved $1,558. She needs at least $2,158 for the repairs. She plans to

add $60 per week to her current savings until she can afford the repairs.
In this activity, you will algebraically model and solve an inequality based on this situation and interpret the solutions within
realistic guidelines
Part A
Question
Given the situation, which inequality models the number of additional weeks Marie needs to continue saving to afford the
home repairs?
Select the correct answer.
1,558 + 60x 22,158
60x + 1,558 5 2,158
1,558 - 60x s 2,158
2,158 - 60x 2 1,558

Answer 1

Its the first one

Explanation:

I just did it lol

Answer 2

Inequality:
`1558 + 60 x \geq 2158`

Number of Weeks:
`x \geq 10`

Explanation:

Given

`Initial\ Savings = \$1558`

`Amount\ Needed = \$2158`

`Additional\ Savings = \$60\ weekly`

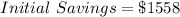
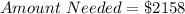
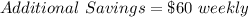
Required

Represent this using an inequality

Represent the number of weeks as x;

This implies that, She'll save $60 * x in x weeks

Her total savings after x weeks would be

`Initial\ Savings + 60 * x`

From the question, we understand that she needs at least 2158;

Mathematically, this can be represented as (greater than or equal to 2158)

`\geq 2158`

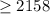
Bringing the two expressions together;

`Initial\ Savings + 60 * x \geq 2158`

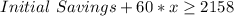
Substitute 1558 for Initial Savings

`1558 + 60 * x \geq 2158`

`1558 + 60 x \geq 2158`

Hence, the inequality that represents the situation is
`1558 + 60 x \geq 2158`

Solving further for x (number of weeks)

`1558 + 60 x \geq 2158`

Subtract 1558 from both sides

`1558- 1558 + 60 x \geq 2158 - 1558`

`60x \geq 600`

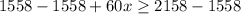
Divide both sides by 60

`(60x)/(60) \geq (600)/(60)`

`x \geq 10`

This means that she needs to save $60 for at least 10 weeks