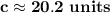Question

In △ABC, m∠A=15 °, a=10 , and b=11 . Find c to the nearest tenth.

Answer 1

The answer is:

`\bold{c\approx 20.2\ units}`

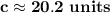
Explanation:

Given:

In △ABC:

m∠A=15°

a=10 and

b=11

To find:

c = ?

Solution:

We can use cosine rule here to find the value of third side c.

Formula for cosine rule:

`cos A = (b^(2)+c^(2)-a^(2))/(2bc)`

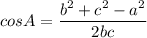
Where

a is the side opposite to
`\angle A`

b is the side opposite to
`\angle B`

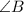
c is the side opposite to
`\angle C`

Putting all the values.

`cos 15^\circ = (11^(2)+c^(2)-10^(2))/(2* 11 * c)\\\Rightarrow 0.96 = (121+c^(2)-100)/(22c)\\\Rightarrow 0.96 * 22c= 121+c^(2)-100\\\Rightarrow 21.25 c= 21+c^(2)\\\Rightarrow c^(2)-21.25c+21=0\\\\\text{solving the quadratic equation:}\\\\c = (21.25+√(21.25^2-4 * 1 * 21))/(2)\\c = (21.25+√(367.56))/(2)\\c = (21.25+19.17)/(2)\\c \approx 20.2\ units`

The answer is:

`\bold{c\approx 20.2\ units}`