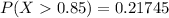Question

According to a study done by the Gallup organization, the proportion of Americans who are satisfied with the way things are going in their lives is 0.82. What is the probability the sample proportion who are satisfied with the way things are going in their life is greater than 0.85

Answer 1

Complete Question

According to a study done by the Gallup organization, the proportion of Americans who are satisfied with the way things are going in their lives is 0.82. Suppose a random sample of 100 Americans is asked "Are you satisfied with the way things are going in your life?"

What is the probability the sample proportion who are satisfied with the way things are going in their life is greater than 0.85

Answer:

The probability is
`P(X > 0.85 ) = 0.21745`

Explanation:

From the question we are told that

The population proportion is
`p = 0.82`

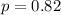
The value considered is x = 0.85

The sample size is n = 100

The standard deviation for this population proportion is evaluated as

`\sigma = \sqrt{(p(1-p))/(n) }`

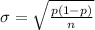
substituting values

`\sigma = \sqrt{(0.82(1-0.82))/(100) }`

`\sigma = 0.03842`

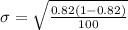
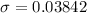
Generally the probability that probability the sample proportion who are satisfied with the way things are going in their life is greater than x is mathematically represented as

`P(X > x ) = P( (X - p )/( \sigma ) > (x - p )/( \sigma ) )`

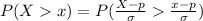
Where
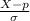`(X - p )/( \sigma )` is equal to Z (the standardized value of X ) so

`P(X > x ) = P( Z> (x - p )/( \sigma ) )`

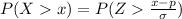
substituting values

`P(X > 0.85 ) = P( Z> ( 0.85 - 0.82 )/( 0.03842 ) )`

`P(X > 0.85 ) = P( Z> 0.78084)`

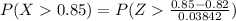
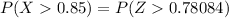
from the standardized normal distribution table
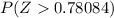`P( Z> 0.78084)` is 0.21745

So

`P(X > 0.85 ) = 0.21745`