Question

A medical equipment industry manufactures X-ray machines. The unit cost (the cost in dollars to make each X-ray machine) depends on the number of machines made. If machines are made, then the unit cost is given by the function . What is the minimum unit cost?Do not round your answer.

Answer 1

$14,362

Explanation:

The computation of the minimum unit cost is shown below:

Given that

0.6x^2 - 108x + 19,222

And as we know that the quadratic equation form is

ax^2 + bx + c

where

a = 0.6

b = -108

c = 19,222

Now for determining the minimal cost we applied the following formula which is

`= (-b)/(2a) \\\\ = (-(-108))/(2* 0.6) \\\\ = (108)/(1.2)`

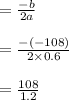
= 90

Now put these values to the above equation

`= 0.6* 90^(2) - 108 * 90 + 19,222`

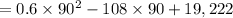
= 14,362