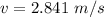Answer:
The velocity is
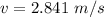
Step-by-step explanation:
The diagram showing this set up is shown on the first uploaded image (reference Physics website )
From the question we are told that
The mass is m = 4 kg
The length of the string is
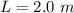
The constant angle is
Generally the vertical forces acting on the mass to keep it at equilibrium vertically is mathematically represented as

=>
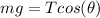
Now let the force acting on mass horizontally be k so from SOHCAHTOA rule
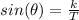
=>

Now this k is also equivalent to the centripetal force acting on the mass which is mathematically represented as

So
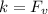
Which
=>
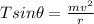
So
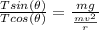
=>
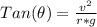
=>
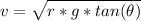
Now the radius is evaluated using SOHCAHTOA rule as

=>
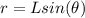
substituting values

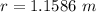
So