Question

Points A,B,C and D are midpoints of the sides of the larger square. If the smaller square has area 60, what is the area of the bigger square?

Answer 1

80

Explanation:

Answer 2

Therefore, the area of the larger square is 120 square units.

Given Information: We're given that the area of the smaller square is 60 square units.

Expressing the Relationship between the Areas:

Let the area of the larger square be represented by
`\( x \)`.

The area of the smaller square is
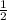`\( (1)/(2) \)` the area of the larger square:

`\[ \text{Area of smaller square} = (1)/(2) * \text{Area of larger square} \]`

Given that the area of the smaller square is 60, we can write:

`\[ 60 = (1)/(2) * x \]`

Solving for the Area of the Larger Square
`(\( x \))`:

Rearrange the equation to solve for
`\( x \)`:

Multiply both sides of the equation by 2 to get rid of the fraction:

`\[ x = 60 * 2 \ \\\\ \[ x = 120`

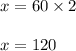
Therefore, the area of the larger square is 120 square units.