Question

1. Notice that the voltmeter moves in response to the coil entering or leaving the magnetic gap.

2. Let's apply Faraday's Law to this situation. Faraday's Law says that the induced voltage (or emf )in a loop of wire caused by a changing magnetic field is:
€ = 1
Where is the magnetic flux which is
Q = BA
In this case, the flux density B is not changing. Instead, the changing flux is due to the motion of the coil as it enters or leaves the magnetic gap:
do = BdA
Given that the area immersed in the gap is changing as the coil enters the gap, what is the correct expression of Faraday's Law for this situation?

Answer 1

Step-by-step explanation:

let the coil of length l and breathe b entering the magnetic field B with speed v.

So, the magnetic flux through the coil is

Ф = B(l×b)

length × breathe = area

Ф = BA

dФ = BdA

therefore induced emf is given as

ε =
`Bl((db)/(dt))`

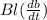
note:
`(db)/(dt) = v`

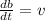
ε
`= Blv`

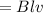
attached is the diagram for the solution