Answer: A)
 = 564.4 N
= 564.4 N
B)
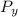 = 374 N
= 374 N
Step-by-step explanation: The ladder forms with the wall a right triangle, with one unknown side. To find it, use Pythagorean Theorem:
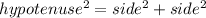

side =

side = 1.65
Tom's weight is a vector pointing downwards. Since he is at an angle to the floor, the gravitational force has two components: one that is parallel to the floor (
 ) and othe that is perpendicular (
) and othe that is perpendicular (
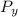 ). These two vectors and weight, which is gravitational force, forms a right triangle with the same angle the ladder creates with the floor.
). These two vectors and weight, which is gravitational force, forms a right triangle with the same angle the ladder creates with the floor.
The image in the attachment illustrates the described above.
A)
 = P sen θ
= P sen θ
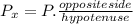
 = 680.
= 680.
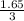
 = 564.4 N
= 564.4 N
B)
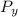 = P cos θ
= P cos θ
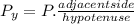
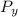 = 680.
= 680.
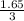
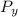 = 374 N
= 374 N