Question

A small meteorite with mass of 1 g strikes the outer wall of a communication satellite with a speed of 2Okm/s (relative to the satellite). The mass of the satellite is 200 kg.

About how much energy (in kJ) was converted to heat?

Answer 1

The energy coverted to heat is 200 kilojoules.

Step-by-step explanation:

GIven the absence of external forces exerted both on the small meteorite and on the communication satellite, the Principle of Linear Momentum is considered and let suppose that collision is completely inelastic and that satellite is initially at rest. Hence, the expression for the satellite-meteorite system:

`m_(M)\cdot v_(M) + m_(S)\cdot v_(S) = (m_(M)+m_(S))\cdot v`

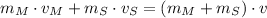
Where:

`m_(M)`,
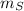`m_(S)` - Masses of the small meteorite and the communication satellite, measured in kilograms.

`v_(M)`,
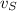`v_(S)` - Speeds of the small meteorite and the communication satellite, measured in meters per second.

`v` - Final speed of the satellite-meteorite system, measured in meters per second.

The final speed of the satellite-meteorite system is cleared:

`v = (m_(M)\cdot v_(M)+m_(S)\cdot v_(S))/(m_(M)+m_(S))`

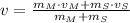
If
`m_(M) = 1* 10^(-3)\,kg`,
`m_(S) = 200\,kg`,
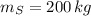`v_(M) = 20000\,(m)/(s)` and
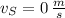`v_(S) = 0\,(m)/(s)`, the final speed is now calculated:

`v = ((1* 10^(-3)\,kg)\cdot \left(20000\,(m)/(s) \right)+(200\,kg)\cdot \left(0\,(m)/(s) \right))/(1* 10^(-3)\,kg+200\,kg)`

`v = 0.1\,(m)/(s)`

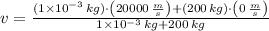
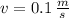
Which means that the new system remains stationary and all mechanical energy from meteorite is dissipated in the form of heat. According to the Principle of Energy Conservation and the Work-Energy Theorem, the change in the kinetic energy is equal to the dissipated energy in the form of heat:

`K_(S) + K_(M) - K - Q_(disp) = 0`

`Q_(disp) = K_(S)+K_(M)-K`

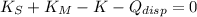
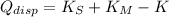
Where:

`K_(S)`,
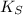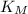`K_(M)` - Initial translational kinetic energies of the communication satellite and small meteorite, measured in joules.

`K` - Kinetic energy of the satellite-meteorite system, measured in joules.

`Q_(disp)` - Dissipated heat, measured in joules.

The previous expression is expanded by using the definition for the translational kinetic energy:

`Q_(disp) = (1)/(2)\cdot [m_(M)\cdot v_(M)^(2)+m_(S)\cdot v_(S)^(2)-(m_(M)+m_(S))\cdot v^(2)]`

Given that
`m_(M) = 1* 10^(-3)\,kg`,
`m_(S) = 200\,kg`,
`v_(M) = 20000\,(m)/(s)`,
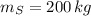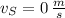`v_(S) = 0\,(m)/(s)` and
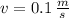`v = 0.1\,(m)/(s)`, the dissipated heat is:

`Q_(disp) = (1)/(2)\cdot \left[(1* 10^(-3)\,kg)\cdot \left(20000\,(m)/(s) \right)^(2)+(200\,kg)\cdot \left(0\,(m)/(s) \right)^(2)-(200.001\,kg)\cdot \left(0.001\,(m)/(s) \right)^(2)\right]`
`Q_(disp) = 200000\,J`

`Q_(disp) = 200\,kJ`

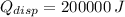
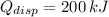
The energy coverted to heat is 200 kilojoules.