Question

Two metal sphere each of radius 2.0 cm, have a center-to-center separation of 3.30 m. Sphere 1 has a chrage of +1.10 10^-8 C. Sphere 2 has charge of -3.60 10^-8C. Assume that the separation is large enough for us to assume that the charge on each sphere iss uniformly distribuuted.

A) Calculate the potential at the point halfway between the centers.
B) Calculate the potential on the surface of sphere 1.
C) Calculate the potential on the surface of sphere 2.

Answer 1

A) V = -136.36 V , B) V = 4.85 10³ V , C) V = 1.62 10⁴ V

Step-by-step explanation:

To calculate the potential at an external point of the spheres we use Gauss's law that the charge can be considered at the center of the sphere, therefore the potential for an external point is

V = k ∑
`q_(i) / r_(i)`

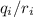
where
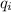`q_(i)` and
`r_(i)` are the loads and the point distances.

A) We apply this equation to our case

V = k (q₁ / r₁ + q₂ / r₂)

They ask us for the potential at the midpoint of separation

r = 3.30 / 2 = 1.65 m

this distance is much greater than the radius of the spheres

let's calculate

V = 9 10⁹ (1.1 10⁻⁸ / 1.65 + (-3.6 10⁻⁸) / 1.65)

V = 9 10¹ / 1.65 (1.10 - 3.60)

V = -136.36 V

B) The potential at the surface sphere A

r₂ is the distance of sphere B above the surface of sphere A

r₂ = 3.30 -0.02 = 3.28 m

r₁ = 0.02 m

we calculate

V = 9 10⁹ (1.1 10⁻⁸ / 0.02 - 3.6 10⁻⁸ / 3.28)

V = 9 10¹ (55 - 1,098)

V = 4.85 10³ V

C) The potential on the surface of sphere B

r₂ = 0.02 m

r₁ = 3.3 -0.02 = 3.28 m

V = 9 10⁹ (1.10 10⁻⁸ / 3.28 - 3.6 10⁻⁸ / 0.02)

V = 9 10¹ (0.335 - 180)

V = 1.62 10⁴ V