Question

Sven starts walking due south at 7 feet per second from a point 190 feet north of an intersection. At the same time Rudyard starts walking due east at 4 feet per second from a point 130 feet west of the intersection.

A. Write an expression for the distance d between Sven and Rudyard t seconds after they start walking.
B. What is the minimum distance between them?
C. When are Sven and Rudyard closest?

Answer 1

Answer: A.
`d=√((190-7t)^2+(130-4t)^2)`

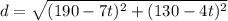
B. Minimum distance between them = 18.61 feet.

C. After 28.76 seconds Sven and Rudyard are closest.

Explanation:

A) Let (0,0) be the intersection point.

Then, Initial Location of Sven (0,190).

Speed of Sven = 7 feet per second

Then, position of Sven after t seconds = (0,190-7t) [speed = distance x time]

Similarly, Initial position of Rudyard= (130,0)

Speed of Rudyard = 4 feet per second

Position after t seconds = (130-4t,0)

Distance d between Sven and Rudyard t seconds after they start walking:

`d=√((190-7t)^2+(130-4t)^2)`

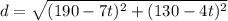
B) Let
`d(t)=√((190-7t)^2+(130-4t)^2)\\`

`d'(t)=2(190-7t)(-7)+(2)(130-4t)(-4)\\\\=130t-3700`

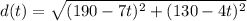
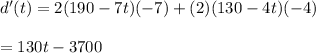
Put d'(t)=0

`130t-3700=0\\\\\Rightarrow\ t=(3700)/(130)\approx28.46\ sec`

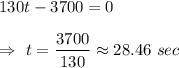
Minimum distance :

`d(28.46)=√((190-7(28.46))^2+(130-4(28.46))^2)\\\\=√(346.154)\approx18.61\ feet`

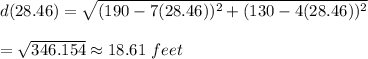
Hence, the minimum distance between them = 18.61 feet.

c) After 28.76 seconds Sven and Rudyard are closest.