Answer:
t = 2.95 min
Step-by-step explanation:
Given that,
The diameter of flywheeel, d = 1.5 m
Mass of flywheel, m = 250 kg
Initial angular velocity is 0
Final angular velocity,
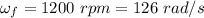
We need to find the time taken by the flywheel to each a speed of 1200 rpm if it starts from rest.
Firstly, we will find the angular acceleration of the flywheel.
The moment of inertia of the flywheel,
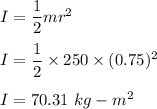
Now,
Let the torque is 50 N-m. So,
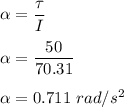
So,
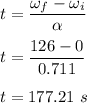
or
t = 2.95 min