Question

Please solve these questions for me. i am having a difficult time understanding.

Answer 1

1) AD=BC(corresponding parts of congruent triangles)

2)The value of x and y are 65 ° and 77.5° respectively

Explanation:

1)

Given : AD||BC

AC bisects BD

So, AE=EC and BE=ED

We need to prove AD = BC

In ΔAED and ΔBEC

AE=EC (Given)

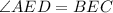`\angle AED = \angel BEC` ( Vertically opposite angles)

BE=ED (Given)

So, ΔAED ≅ ΔBEC (By SAS)

So, AD=BC(corresponding parts of congruent triangles)

Hence Proved

2)

Refer the attached figure

`\angle ABC = 90^(\circ)`

In ΔDBC

BC=DC (Given)

So,
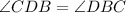`\angle CDB=\angle DBC`(Opposite angles of equal sides are equal)

So,
`\angle CDB=\angle DBC=x`

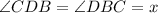
So,
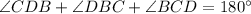`\angle CDB+\angle DBC+\angle BCD = 180^(\circ)` (Angle sum property)

x+x+50=180

2x+50=180

2x=130

x=65

So,
`\angle CDB=\angle DBC=x = 65^(\circ)`

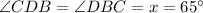
Now,

`\angle ABC = 90^(\circ)\\\angle ABC=\angle ABD+\angle DBC=\angle ABD+x=90`

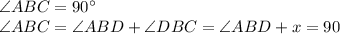
So,
`\angle ABD=90-x=90-65=25^(\circ)`

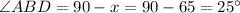
In ΔABD

AB = BD (Given)

So,
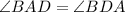`\angle BAD=\angle BDA`(Opposite angles of equal sides are equal)

So,
`\angle BAD=\angle BDA=y`

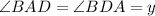
So,
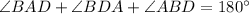`\angle BAD+\angle BDA+\angle ABD = 180^(\circ)`(Angle Sum property)

y+y+25=180

2y=180-25

2y=155

y=77.5

So, The value of x and y are 65 ° and 77.5° respectively