Answer: (84.876, 87.124)
Explanation:
Confidence interval for population mean if population standard deviation is unknown:
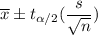
, where n= sample size
s= sample standard deviation
 = sample mean
= sample mean
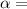 significance level
significance level
 = critical-t value
= critical-t value
Given: n= 64
Degree of freedom = n-1 = 63
s= 4.5
 = 86
= 86
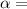 0.05
0.05
 = 1.9983
= 1.9983
Now, the required 95% confidence interval would be:
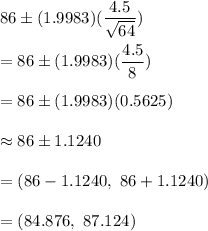
The 95% confidence interval for the population mean μ is between: (84.876, 87.124)