Question

A shipping container is in the shape of a cube and has a side length of 6ft. It can hold 4 smaller boxes of flour.

If the dimensions of the shipping container are tripled, what is the max number of smaller boxes of flour that the shipping box can hold

Answer 1

c. 108

Explanation:

Given

Shape of container: Cube

Initial dimension of the container = 6ft by 6ft by 6ft

Initial Number of boxes = 4

Required

Calculate the number of boxes when the dimension is tripled

The first step is to calculate the initial volume of the box;

`Volume = Length * Length * Length`

`Volume = 6ft * 6ft * 6ft`

`Volume = 216ft^3`

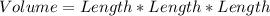
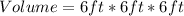
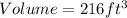
This implies that the container can contain 4 small boxes when its volume is 216;

Represent this as a ratio;

`4 : 216`

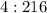
The next step is to calculate the volume when the dimension is tripled;

`New\ Length = Old\ Length * 3`

`New\ Length = 6ft* 3`

`New\ Length = 18ft`

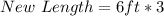
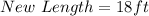
Hence;

`Volume = 18ft * 18ft * 18ft`

`Volume = 5832ft^3`

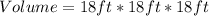
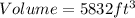
Let the number of boxes it can contain be represented with x

Similarly, represent this as a ratio

`x : 5832`

Equate both ratios;

`4 : 216 = x : 5832`

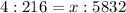
Convert ratios to fractions

`(4)/(216) = (x)/(5832)`

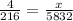
Multiply both sides by 5832

`5832 * (4)/(216) = (x)/(5832) * 5832`

`5832 * (4)/(216) = x`

`(5832 *4)/(216) = x`

`(23328)/(216) = x`

`108 = x`

`x = 108`

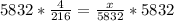
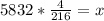
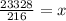
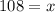
Hence, the maximum number of boxes it can contain is 108