Question

Six human skulls from around 4000 b.c. were measured, and the lengths have a mean of 94.2 mm and a standard deviation of 4.9

mm. If you want to construct a 95% confidence interval estimate of the mean length of all such skulls, assume that the requirements
are satisfied. Find the critical values that would be used to construct a 95% confidence interval estimate of o

Answer 1

Explanation:

Hello!

You have to estimate the mean length of 4000 b.c. human skulls trough a 95% confidence interval.

You know that

n= 6 human skulls

`\frac{}{X}`= 94.2mm

S= 4.9

Assuming that the variable X: length of a 4000b.c. human skull (mm) has a normal distribution, to construct the interval you have to use the t statistic:

[
`\frac{}{X}` ±
`t_(n_1;1-\alpha /2) * (S)/(√(n) )`]

`t_(n-1;1-\alpha /2)= t_(5; 0.975)= 2.571`

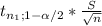[94.2 ± 2.571 *
`(4.9)/(√(6) )`]

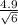[89.06; 99.34]mm

With a 95% confidence level you'd expect the interval [89.06; 99.34]mm to contain the value for the average skull length for humans 4000 b.c.

I hope this helps!