Question

Kathryn's school is selling tickets to a choral performance. On the first day of ticket sales the school sold 6 adult tickets and 11 student tickets for a total of $118. The school took in $156 on the second day by selling 12 adult tickets and 12 student tickets. What is the price of each adult ticket? What is the price of each student ticket?

Answer 1

Adult price $5

Student price 8$

Explanation:

Hello!

The school sells tickets for the choral performance with different prices depending on the ticket is for an adult or for a student of the school.

If X represents the price of an adult ticket and Y represent the price of a student ticket using the given information you can determine a set of two equations with two unknown values:

Day 1: 6 adult tickets and 11 student tickets for a total of $118

Symbolically: 6X + 11Y= $118

Day 2: 12 adult tickets and 12 student tickets for a total of $156

Symbolically: 12X + 12Y= $156

Step 1

From one of the formulas, clear one of the unknown values:

`12X + 12Y= 156\\12Y= 156- 12X\\Y= (156-12X)/(12) \\Y= 13 - X`

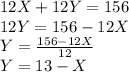
Step 2

Replace the value obtained in step one in the second formula:

`6X + 11Y= 118\\6X + 11(13 - X)= 118\\6X + (11*13) - 11X = 118\\6X -11X + 143= 118\\-5X= 118 - 143\\-5X= -25\\X= 5`

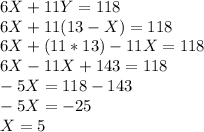
The ticket price for an adult is $5

Step 3

Using the value of X obtained in step 2, replace in the formula for Y to obtain the ticket price for students:

Y= 13 - X= 13 - 5= $8

I hope this helps!