Question

Starting from an airport, an airplane flies 290 miles east and then 290 miles northwest. How far, in miles, from the airport is the plane? (Round your answer to the nearest mile.)

Answer 1

The airplane is 222 miles far from the airport.

Explanation:

After a careful reading of the statement, distances can be described in a vectorial way. A vector is represented by a magnitude and direction. That is:

Airplane flies 290 miles (east) (290 km with an angle of 0º)

`\vec r_(A) = (290\,mi)\cdot i`

Airplane flies 290 miles (northwest) (290 km with and angle of 135º)

`\vec r_(B) = [(290\,mi)\cdot \cos 135^(\circ)]\cdot i + [(290\,mi)\cdot \sin 135^(\circ)]\cdot j`

The resultant vector is equal to the sum of the two vectors:

`\vec r_(C) = \vec r_(A) + \vec r_(B)`

`\vec r_(C) = \{(290\,mi) + \left[(290\,mi)\cdot \cos 135^(\circ)\right]\}\cdot i + \left[(290\,mi)\cdot \sin 135^(\circ)\right]\cdot j`

`\vec r_(C) = (84.939\,mi)\cdot i + (205.061\,mi)\cdot j`

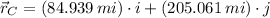
The magnitude of the final distance of the airplane from the airport is obtained by the Pythagorean Theorem:

`\|\vec r_(C)\|=\sqrt{(84.939\,mi)^(2)+(205.061\,mi)^(2)}`

`\|\vec r_(C)\| = 221.956\,mi`

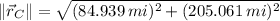
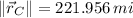
The airplane is 222 miles far from the airport.