Question

Salaries of 43 college graduates who took a statistics course in college have a​ mean,66,000 ​, of . Assuming a standard​ deviation, 18908 ​, of ​$​, construct a ​%99 confidence interval for estimating the population mean .

Answer 1

$[58543.42; 73456.58]

Explanation:

Hello!

For the variable

X: salary of a college graduate that took a statistics course

Out of n= 43 students, the calculated mean is
`\frac{}{X}`= $66000

The population standard deviation is δ= $18908

There is no information about the variable distribution, but since the sample size is big enough (n≥30), you can apply the CLT and approximate the distribution of the sample mean to normal
`\frac{}{X}`≈N(μ;σ²/n)

Then you can apply the approximation of the standard normal distribution to calculate the 99% CI

`\frac{}{X}` ±
`Z_(1-\alpha /2)` *
`(Singma)/(√(n) )`

`Z_(1-\alpha /2)= Z_(0.995)= 2.586`

`(Singma)/(√(n) )= (18908)/(√(43) )= 2883.44`

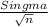
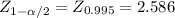
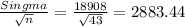
[66000±2.586*2883.44]

$[58543.42; 73456.58]

With a 99% confidence level you'd expect that the interval $[58543.42; 73456.58] will include the average salary of college graduates that took a course of statistics.

I hope this helps!