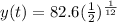Answer:
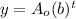
With
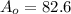 the initial amount and t the time on hours and t the time in hours. since the half life is 12 hours we can find the parameter of decay like this:
the initial amount and t the time on hours and t the time in hours. since the half life is 12 hours we can find the parameter of decay like this:
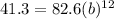
And solving for b we got:
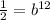
And then we have:
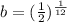
And the model would be given by:
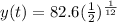
Explanation:
Assuming this complete question: "A specific radioactive substance follows a continuous exponential decay model. It has a half-life of 12 hours. At the start of the experiment, 82.6g is present. "
For this case we can create a model like this one:
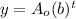
With
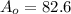 the initial amount and t the time on hours and t the time in hours. since the half life is 12 hours we can find the parameter of decay like this:
the initial amount and t the time on hours and t the time in hours. since the half life is 12 hours we can find the parameter of decay like this:
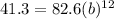
And solving for b we got:
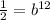
And then we have:
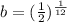
And the model would be given by: